Random Forest

Random Forest其实就是在Bagging的基础上添加随机属性，Bagging Tree就是基于Bootstrape训练多个Tree。下面将一一进行展开

Bagging Tree

Bagging Tree就是基于Bootstrape生成多个训练集，然后基于这些训练集得到多个CART，检测时使用这多个CART进行检测，即:
$\hspace{4mm}F_{bag}(x) = \sum\limits_{b=1}^{B}f(x)$

• Bootstrape
  假设有训练集有N个样本，则在这N个样本中随机挑训N个样本作为新的训练集(其可以有重复)，如下:
  

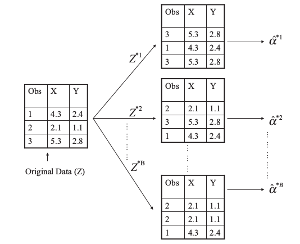
• 重点

  1. Bagging Tree的每一个子树不需要Prune，其是通过平均多个子树来降低Variance的
  2. Bagging的缺点是可能其每一个子树都比较相似，导致最终并不能带来很大的提高(Random Fores很好的解决了这个问题)
  3. 实验表明，每次bootstrape生成的样本只占训练集的2/3。其他1/3的部分可以用来测试
     
     

Random Forest

Random Forest就是在Bagging tree的基础上增加了随机的属性。即在构建树时，每次用来进行分割的特征是随机选择的一个子集，而不是所有特征。因此就算完全一样的训练，其生成的树也是不同的。有效的解决了Bagging Tree中的子树相似的问题

Random Ferns

单个Fern的构建：假设有D为特征，则随机挑选S个特征，并在这S个特征上随机的挑选一个阈值进行分割。则最终有$2^S$个leaf节点。Random Ferns即将多个Ferns结合在一起,详细见文章[2]

Boosting Tree

Boosting Tree用在回归上时，是不断的减少检测值与真实值之间的residual。分类时，其比较复杂，暂时不提供

• Regression

1. Set f(x) = 0 and $r_i = y_i$ for all i in the training set.
2. For b = 1, 2, . . . , B, repeat:
   a). Fit a tree $f^b$ with d splits (d+1 leafs) to the training data(X, r)
   b). Update f by adding in a shrunken version of the new tree:
   $\hspace{8mm}f(x) ← f(x) + \lambda f^b(x)$
   c). Update the residuals:
   $\hspace{8mm}r_i ← r_i − \lambda f^b(x_i)$(r为residual即真实值与预测值之间的差)
3. Output the boosted model:
   $\hspace{8mm}f(x) = \sum\limits_{b=1}^{B}\lambda f^b(x)$

• Classification
  Coming soon
  
  

References

1. An Introduction to Statistical Learning with Applications in R
2. Fast keypoint recognition using random ferns