PMK(Pyramid Match Kernels)

2006年由Kristen Grauman在文章[1]中提出来的算法,其适用于 unordered、unequal length features

• Algorithm:
  假设特征$x\in R^{d \times m_x}$,即为d维，且每一维的长度为$m_x$(每个特征的长度可以不一样),即:
  $\hspace{4mm}X = \{x | x = {[f_1^1,...,f_d^1];...;[f_1^{m_x},...,f_d^{m_x}]}\}$
  
  这里特征值必须为整数,假设特征值$f \in (1，D)$，这里直方图bin的宽度以 2的倍数 增加，则直方图的分辨率$L=log_2D$，那么
  $\hspace{4mm}H_0(x)的直方图的bin宽度为1 \\ \hspace{4mm}H_l(x)的直方图的bin宽度为2^l，其维度为(\frac{D}{2^l})^d$
  则所有分辨率组合到一起的特征为:
  $\hspace{4mm}\Psi (x)=[H_{-1}(x),H_0(x),...,H_L(x)] \\ \hspace{8mm}(H_{-1}(x)只是为了占位，其实不存在)$
  
  则PMK的相似度定义如下:
  $\hspace{4mm}K(\Psi (x), \Psi (y)) = \sum_{i=0}^Lw_iN_i \hspace{16mm}(1)\\ \hspace{8mm}其中:\\ \hspace{12mm}w_i=\frac{1}{2^i} \\ \hspace{12mm}N_i= I(H_i(x), H_i(y)) - I(H_{i-1}(x), H_{i-1}(y)) \\ \hspace{12mm}I(H_{-1}(x), H_{-1}(y))=0 \\ $
  一维特征的PMK图形示例如下:
  
  
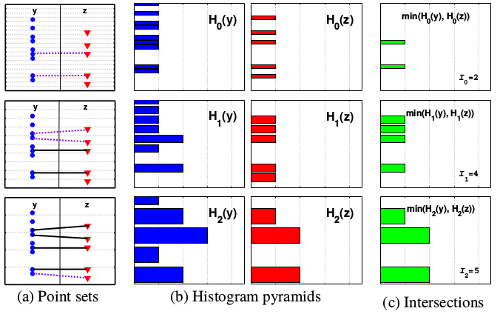
  Normalized Version 1:
  $\hspace{4mm}K_{normalize}(\Psi (x), \Psi (y)) = \frac{K(\Psi (x), \Psi (y))}{min(|x|_{1_norm}，|y|_{1_norm})} \hspace{16mm}(2)$
  
  Normalized Version 2:
  $\hspace{4mm}K_{normalize}(\Psi (x), \Psi (y)) = \frac{K(\Psi (x), \Psi (y))}{\sqrt{K_{normalize}(\Psi (x), \Psi (x))*K_{normalize}(\Psi (y), \Psi (y))}}\hspace{16mm}(3)$

• 说明:
  
  1. $I(H_i(x), H_i(y))$为Histogram Intersection.
  2. $N_i$需要减去前一层相交,因为前一层的相交在后一层中也相交 .
  3. $w_i$是根据直方图bin的个数来的。d维边长为$2^i$的超立方体点之间的最大距离为$2^i\sqrt{d}$ 。 因为i+1层的直方图的bin为i层的一半(即i+1层最大距离是i层的一半)，因此$N_{i+1}$的权重也为$N_{i}$的一半。 即直方图越精细其权重也越大
• 补充说明:
  文章中作者为了解决直方图量化时不同的偏移引入的问题，如下图: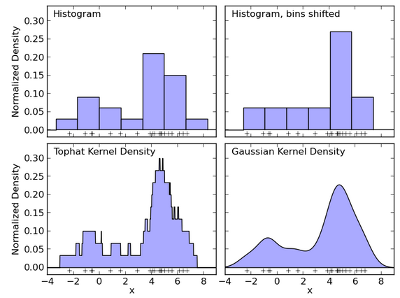
  作者在直方图量化时采用多次随机偏移来解决这个问题，即:
  $\hspace{4mm}\sum_{j=0}^TK(\Psi_j (x), \Psi_j (y))$
  
  

Spatial Pyramid Matching

2006年Svetlana Lazebnik在文章[2]中基于文章[1]提出引入空间的信息,即按照 图像的位置信息 来量化直方图，方法如下:

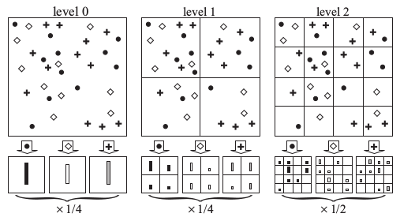
作者在这里引入M中类型的特征，且每个的类型的特征都是2-d的图像，则其公式如下:
$\hspace{4mm}K = \sum_{i=0}^MK(\Psi (x_i), \Psi (y_i)) \hspace{16mm} (4)$

• 说明
  
  1. 上图中M=3(圆形，菱形，加号)。
  2. 理论上 可以将上面的PMK的特征$x\in R^{d \times m_x}$直接当成一个2-d的图像来量化，此时M=D.
  3. 特征的总维度为$M\sum\limits_{l=0}^{L}4^l$
     
     
• Beyond BOW
  文章中作者提出一种超过BOW的特征。基于很多子图像块使用聚类算法，先聚出如200个中心点(即M=200)。然后每幅图像进行二维扫描得到每个子块属于哪个类的索引。基于这个2-D的索引图，得到每个金字塔层的直方图。
  

References

1. Pyramid Match Kernels: Discriminative Classification with Sets of Image Features
2. Beyond bags of features: spatial pyramid matching for recognizing natural scene categories