RBM(Restricted Boltzmann Machine)

RBM是一个无向图(Undirected Graph)模型，其结构如下:

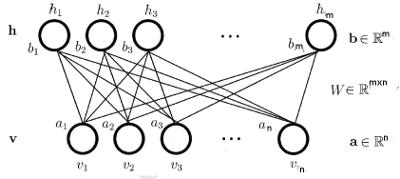
Bernoulli-Bernoulli RBM

• RBM模型结构
  此时可视层节点和隐层节点均为二值变量。即$v_i \in \{0,1\}$, $h_i \in \{0,1\}$，此时的 能量方程 为:
  $\hspace{4mm}E(\mathbf{v,h}|\theta) = -\sum\limits_{i=1}^{n}a_iv_i - \sum\limits_{j=1}^mb_jh_j - \sum\limits_{i=1}^n\sum\limits_{j=1}^mv_iW_{ij}h_j \\ \hspace{8mm}其中: \\ \hspace{12mm}\theta = \{W_{ij}, a_i, b_j\} \\ \hspace{12mm}a_i为可视层的偏置(bias) \\ \hspace{12mm}b_i为隐层的偏置(bias)$
  
  则($\mathbf{v,h}$)的 联合概率分布 为:
  $\hspace{4mm}P(\mathbf{v,h}|\theta) = \frac{e^{-E(\mathbf{v,h}|\theta)}}{Z(\theta)}\\ \hspace{8mm}其中: \\ \hspace{12mm}Z(\theta) = \sum\limits_{\mathbf{v,h}}e^{-E(\mathbf{v,h}|\theta)}$
  由于(v,h)是二值的因此计算$Z(\theta)$,需要$2^{m+n}$次计算，其计算量太大无法在有效的时间内求得，因此其联合概率分布不可以直接求得。
  
  因为隐层与可视层层内无连接, 因此每个节点是条件独立的，即: $\hspace{4mm}P(h_j=1|v,\theta) = \sigma(b_j+\sum\limits_iv_iW_{ij}) \\ \hspace{4mm}P(v_i=1|h,\theta) = \sigma(a_i+\sum\limits_jW_{ij}h_j) \\ \hspace{8mm}其中: \\ \hspace{12mm}\sigma(x) = \frac{1}{1+exp(-x)}$

• 基于对比散度的学习原理
  通过最大化RBM在训练集上(样本数为T)的对数似然函数，学习得到参数$\theta$，即:
  $\hspace{4mm}\theta ^* = argmax\{L(\theta)\} \\ \hspace{4mm}L(\theta) = \sum\limits_{t=1}^{T}logP(\mathbf{v}^t|\theta) = \sum\limits_{t=1}^{T}log\sum\limits_{\mathbf{h}}P(\mathbf{v}^t,\mathbf{h}|\theta) \\ \hspace{13mm} = \sum\limits_{t=1}^Tlog\frac{\sum_\mathbf{h}exp[-E(\mathbf{v}^t,\mathbf{h}|\theta)]}{\sum_\mathbf{v}\sum_{\mathbf{h}}exp[-E(\mathbf{v},\mathbf{h}|\theta)]} \\ \hspace{13mm} = \sum\limits_{t=1}^T(log{\sum_\mathbf{h}exp[-E(\mathbf{v}^t,\mathbf{h}|\theta)]}-log{\sum_\mathbf{v}\sum_{\mathbf{h}}exp[-E(\mathbf{v},\mathbf{h}|\theta)])} \\ $
  使用梯度法求解上式时，上式对$\theta$的求导如下:
  $\hspace{4mm}\frac{\partial L}{\partial \theta} = \sum\limits_{t=1}^T\frac{\partial}{\partial \theta}(log{\sum_\mathbf{h}exp[-E(\mathbf{v}^t,\mathbf{h}|\theta)]}-log{\sum_\mathbf{v}\sum_{\mathbf{h}}exp[-E(\mathbf{v},\mathbf{h}|\theta)])} \\ \hspace{10mm}=\sum\limits_{t=1}^T\{\sum\limits_h(\frac{exp[-E(\mathbf{v}^t,\mathbf{h}|\theta)]}{\sum\limits_hexp[-E(\mathbf{v}^t,\mathbf{h}|\theta)]}\times\frac{\partial(-E(\mathbf{v}^t,\mathbf{h}|\theta))}{\partial\theta}) - \sum\limits_v\sum\limits_h(\frac{exp[-E(\mathbf{v},\mathbf{h}|\theta)]}{\sum\limits_v\sum\limits_hexp[-E(\mathbf{v},\mathbf{h}|\theta)]}\times\frac{\partial(-E(\mathbf{v},\mathbf{h}|\theta))}{\partial\theta})\} \\ \hspace{10mm}=\sum\limits_{t=1}^T(<\frac{\partial(-E(\mathbf{v}^t,\mathbf{h}|\theta))}{\partial\theta}>_{P(\mathbf{h|v}^t,\theta)} - <\frac{\partial(-E(\mathbf{v},\mathbf{h}|\theta))}{\partial\theta}>_{P(\mathbf{v,h}|\theta)}) \\ \hspace{4mm}\textbf{其中}: \\ \hspace{8mm}<.>_p 表示基于分布P的期望$
  
  用data和model来间记$P(\mathbf{h|v}^t,θ)$和$P(\mathbf{h, v}|θ)$这两个概率分布, 则(当对某一个变量求偏导时，其他项就都被约掉了)
  $\hspace{4mm}\frac{\partial logP(\mathbf{v}|\theta)}{\partial W_{ij}} = <v_ih_j>_{data}-<v_ih_j>_{model}\\ \hspace{4mm}\frac{\partial logP(\mathbf{v}|\theta)}{\partial a_{i}} = <v_i>_{data}-<v_i>_{model} \\ \hspace{4mm}\frac{\partial logP(\mathbf{v}|\theta)}{\partial b_{j}} = <h_j>_{data}-<h_j>_{model} \\ $
  由上面知，联合概率分布不可求，因此上式中的第二项不可以直接求，可以通过Gibbs采样来近似。但通常情况下需要使用较大的采样步数，这使得RBM的训练效率仍旧不高，2002年hinton于文章[2]中提出了Constrastive Divergence, 即使用基于训练样本的重构数据来近似联合分布
  
  $\hspace{4mm}\frac{\partial logP(\mathbf{v}|\theta)}{\partial W_{ij}} = <v_ih_j>_{data}-<v_ih_j>_{recon}\\ \hspace{4mm}\frac{\partial logP(\mathbf{v}|\theta)}{\partial a_{i}} = <v_i>_{data}-<v_i>_{recon} \\ \hspace{4mm}\frac{\partial logP(\mathbf{v}|\theta)}{\partial b_{j}} = <h_j>_{data}-<h_j>_{recon} \\ $
  
  其训练的详细步骤如下(使用的是$CD_1$,即只做了一次的重构，其可以是多次)
  
  
  

Gaussian-Bernoulli RBM

见文章[3]，其能量方程如下:
$\hspace{4mm}E(\mathbf{v,h}|\theta) = \sum\limits_{i=1}^{n}\frac{(v_i-a_i)^2}{2{\sigma}_i^2} - \sum\limits_{j=1}^mb_jh_j - \sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac{v_i}{\sigma_i}W_{ij}h_j \\ \hspace{8mm}其中: \\ \hspace{12mm}\sigma_i为可视层节点i的高斯噪声的标准差$

1. 可以在训练之前，将样本进行标准差归一化，这样$\sigma_i$就可以设为1
2. 隐层重构可见层时，直接用其线性的输出值，就不需要加激活函数了
3. 学习率要小一点，因为从隐层重构到可视层的值是没界的，会导致梯度值很大

疑问1：v不是二值的，导数的第二项是不是要基于所有的v进行积分吗？

Gaussian-Gaussian RBM

见文章[3]，其能量方程如下:
$\hspace{4mm}E(\mathbf{v,h}|\theta) = \sum\limits_{i=1}^{n}\frac{(v_i-a_i)^2}{2{\sigma}_i^2} + \sum\limits_{j=1}^{m}\frac{(h_j-b_j)^2}{2{\sigma}_j^2} - \sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac{v_i}{\sigma_i}W_{ij}\frac{h_j}{\sigma_j} \\ \hspace{8mm}其中: \\ \hspace{12mm}\sigma_i为可视层节点i的高斯噪声的标准差\\ \hspace{12mm}\sigma_j为可视层节点i的高斯噪声的标准差$
其模型比较不稳定，学习起来较困难

疑问2：v,h不是二值的，导数的第一，第二项不是要基于所有的v和h进行积分了吗？

Reference

1. 受限波尔兹曼机简介 张春霞
2. Training products of experts by minimizing contrastive divergence
3. A Practical Guide to Training Restricted Boltzmann Machines