KMean

Classic k-means

• loss function(Minimize the within-cluster variation)
  $\hspace{4mm}J(c^{(1)}, ..., c^{(M)}, u_1, ..., u_K)＝\frac{1}{2M}\sum\limits_{i=1}^{m}{|x^{(i)} - u_{c^{(i)}}|^2} \\ \hspace{8mm}其中: \hspace{12mm}u_k 是聚类中心点的位置 \\ \hspace{12mm}c^{(m)} 是第m个样本其归属类的索引（1-K）$
  其目标函数每次迭代完必须是下降的，否则代码有 bug , 如下图:
  
  
  
• EM Train
  
  1. 随机选择K个聚类中心点（$u_1,..u_k ...u_K$）(cluster centroids)
     一般做法是从训练样本中随机抽取K个样本作为聚类中心点
  2. 找到每个训练样本其最近的聚类中心点$u_k$，并将其归属到第k类 最近点通过$min_k|x-u_k|^2$ 计算
  3. 将每个类中的样本求均值， 将其均值点当成新的聚类中心点
  4. '’repeat 2,3 until convergence’’
     
     
• Tips
  
  1. 避开局部最小(Local optimal) K-means的结果严重依赖与初始化的聚类中心点。
     a. 类比较少的情况， 如2-10个类，可以通过随机多次初始点进行多次训练选取最小的J作为最终的解决方案
     b. 类比较多的情况， 如100个类，随机多次训练就不合适了，TODO: 解决方案
  2. 在上面的第2，3步中， 可能有的类中没有样本， 这样就没法计算平均位置
     a. 传统做法，将这个类删除，这样就只有K-1个类了
     b: 重新进行初始化，再开始训练
  3. 类多的J肯定比类少的J要小， 否则类多的一定是收敛到了local optimal
     
     
• set K
  
  1. elbow method, 通过拐点来寻找，通常情况下 工作得不是很好 ,因为其图形多数情况下，更像右边没有拐点
     
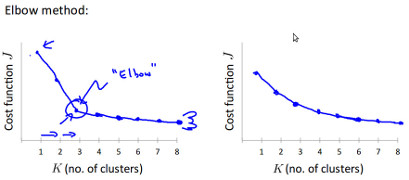
  2. 根据需要来设定类的个数

Hierarchical Clustering

• 原理
  
  1. 首先每个样本都是一个类（则此时有N个类）
  2. 在这N个类中寻找最相似的两个类进行合并，（则此时有N-1个类）
  3. 在这N-1个类中寻找最相似的两个类进行合并，（则此时有N-2个类）
  4. 重复上面的步骤，直到最后只有一个类
• 属性
  1. 与KMean不同，其不需要设置K
  2. 可以动态的选择K的个数，如下图，在特定的高度处进行cut，就会得到特定的类数
     

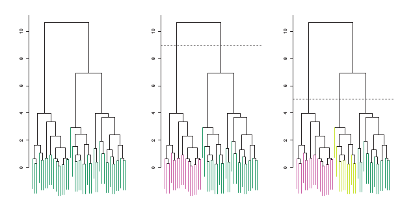
References

1. An Introduction to Statistical Learning