Linear Algebra

学习的是MIT的Introduction to Linear Algebra(Gilbert Strang)，其公开课的视频可以在网易公开课上找到。个人人为其是线性代数的最好(没有之一)的教程了

第一章(Introduction to Vectors)要点

---

• 矩阵与向量的相乘用矩阵列空间的线性组合来表示
  $\left(\begin{array}{c}1&2&9\\3&4&2\\2&5&0\end{array}\right)* \left(\begin{array}{c}1\\2\\3\end{array}\right)= 1*\left(\begin{array}{c}1\\3\\2\end{array}\right)+ 2*\left(\begin{array}{c}2\\4\\5\end{array}\right)+ 3*\left(\begin{array}{c}9\\2\\0\end{array}\right)$
  
  

第二章(Solving Linear Equations)要点

---

• 高斯消元
  将矩阵转换成上三角矩阵U
• 通过Gauss-Jordan消元求逆矩阵。
  理论依据为$A^{-1}[A\hspace{4mm}I] = [I\hspace{4mm}A^{-1}]$
• A=LU分解。
  任意一个矩阵都可以进行LU分解。其中L是主对角线上元素为1的下三角矩阵，U为上三角矩阵，其主对交线上的元素为pivot。有时候其分解需要进行行交换，则使用PA=LU形式。Matlab中使用[L,U]=lu(A)或[L,U,P]=lu(A)。
  
  

第三章(Vector Spaces and Subspaces)要点

---

• 零空间
  即$A * \vec x=0$的所有解$\vec x$
• 矩阵的秩 行秩==列秩
• $A * \vec x= \vec b$的所有解 解为其特解与零空间的组合
• 空间的基与维数
• 四个空间：列空间、零空间、行空间、左零空间
  其中行空间和零空间互为正交补，列空间和左零空间互为正交补
  
  

第四章(Orthogonality)要点

---

• 投影
  
  1. 投影矩阵的推导 假设求$\vec b$在A列空间S上的投影$\vec p$，如下图：
     
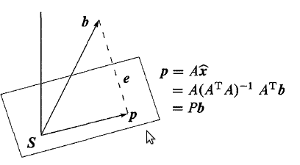
     因为$\vec e = \vec b - \vec p$是垂直与其列空间S，则
     $\hspace{8mm}A^T\vec p = A^T(\vec b - A\vec x)=0 \\ \hspace{8mm}A^T\vec b = A^TA\vec x \\ \hspace{8mm}则\hspace{4mm} \vec x = (A^TA)^{-1}A^T\vec b \\ \hspace{8mm}投影向量\hspace{4mm} \vec p = A\vec x = A(A^TA)^{-1}A^T\vec b \\ \hspace{8mm}投影矩阵\hspace{4mm} P = A(A^TA)^{-1}A^T$
     当A的列向量为正交基时，$\vec x$可以理解为$\vec p$在A列空间中的坐标
  2. 主要应用是来解决$A*\vec x=\vec b$没有解，只能求其最优解。即两边乘以$A$的转置$A^T$变成$A^TA\vec x_*=A^T\vec b$ ，其实 $A\vec x_*$ 就是$\vec b$在A列空间中的投影。 $A^TA$可逆时$\vec x=(A^TA)^{-1}A^T\vec b$，不可逆时通过消元来求解。
  3. $A^TA$可逆的充要条件是A的列线性无关
  4. 最小二乘直线拟合(求其倒数，使其导数为0，得到一些列等式构造出$A*\vec x=\vec b$)、基于squared error的线性回归也可以使用投影的理论来求解(也叫 normal equation )等等
• 使用Gram-Schmidt方法在独立的向量上求其正交基的步骤
  注意Gram-Schmidt的条件是其向量必须线性独立
• A=QR分解
  当A的列向量线性独立的时候，其可以进行QR分解，Q为其正交基向量，R为上三角矩阵
  
  

第五章(Determinats)要点

---

• 10个属性
  1. det(I) = 1
  2. 行交换或列交换会导致行列式值的符号的改变
  3. $\left(\begin{array}{c}ta&tb\\c&d\end{array}\right) = t\left(\begin{array}{c}a&b\\c&d\end{array}\right) \\ $
     $\left(\begin{array}{c}a+a_1&b+b_1\\c&d\end{array}\right) = \left(\begin{array}{c}a&b\\c&d\end{array}\right) + \left(\begin{array}{c}a_1&b_1\\c&d\end{array}\right)$
  4. 如果矩阵A中有相同的行或相同的列，其det(A)=0
  5. 行或列的线性变换不改变行列式的值，如$\left(\begin{array}{c}a+lc&b+ld\\c&d\end{array}\right) = \left(\begin{array}{c}a&b\\c&d\end{array}\right)$
  6. 矩阵中有0行或0列，则其det=0
  7. 三角矩阵的det等于其主对角线上元素的乘积
  8. $det(A) = \pm det(U)$，其中U为A进行LU分解后的U矩阵
  9. det(AB) = det(A)det(B)
  10. det(A) = $det(A^T)$
• pivot可以通过行列式得到
• 通过余子式（cofactor）。得到行列式的计算公式
• Cramer法则求解Ax=b
  
  

第六章(Eigenvalues and Eigenvectors)要点

---

• 特征值于特征向量的求解公式
  A$\vec x = \lambda \vec x$
• $A^n$的特征向量于A的相同，但是其特征值是A的n次方
• $A+ aI$的特征值等于A的特征值加a
  注意A+B的特征值不等于其各自的特征值的和
• 特征值的和等于主对角线上元素的和，特征值的积等于其行列式
• 特征值与特征向量可以是虚数
  如矩阵[0,-1; 1, 0]
• 三角矩阵的特征值就其对角线上的元素
• nxn的对称矩阵的特征值可以重复，但是其肯定有n个正交基
• 正定矩阵
  
  1. 当A的所有特征值大于0时其为正定矩阵
  2. 当R的列向量线性独立时，$R^TR$是正定矩阵
• SVD分解
  $\hspace{4mm}A = U\sum V^T \\ \hspace{8mm}其中: \\ \hspace{12mm}U是AA^T的正交特征向量 \\ \hspace{12mm}V是A^TA的正交特征向量 \\ \hspace{12mm}\sum是AA^T或A^TA特征值的平方根形成的对角矩阵$
  matlab中svd函数求的也是上面的U，$\sum$，V。当A是对称矩阵时，其$A^TA=A^2$,因此U，V相同且其也是A的特征向量。因此在PCA中求协方差矩阵A的特征值与特征向量时用的也是svd(A'A),其$\sum$正好就是其特征值(这里假设了A列向量线性独立，即A'A是正定矩阵)
  
  

第七章(Linear Transformations)要点

---

• 左右逆、伪逆
  $左逆: \\ \hspace{4mm}A^{-1}A = I \\ 右逆: \\ \hspace{4mm}AA^{-1} = I \\ 当A的逆不存在时，其伪逆为: \\ \hspace{4mm}A^+=V\sum^+U^T=[v_1 ... v_n]\left(\begin{array}{c}\sigma_1^{-1}&&\\&...&\\&&\sigma_n^{-1}\end{array}\right)[u_1 ... u_n]^T$