Training Tricks for Neural Network

本文主要就Neural Network的一些训练技巧进行简单的总结

Stochastic versus Batch learning

• Pros of Stochastic Learning
  
  1. 学习过程比Batch Learning快
     假设样本集中有10个样本，然后每个样本生成9个自身的copy，这样就有100个样本。 Stochastic只需要10个样本就完成了一个epoch。 而Batch则需要计算100个样本才能完成一次epoch(而且其中90次是无用的计算)
  2. 学习的效果一般比较好
     因为Stochastic的过程比较振荡，容易跳过一些局部最小值，找到更好的局部最小值。而Batch在初始参数定了以后其最终的局部最小值就定了
  3. 可以用来跟踪学习样本的变化
     样本的变化，会立即反应到训练中，这也是其另一个名字Online Lerning的由来
• Pros of Batch Learning
  
  1. 学习的过程比较平稳
     Batch的学习过程比较平稳，容易收敛，而Stochastic比较振荡，因此一般Stochastic的学习率都比较小。可以采用mini-batch来折衷，既可以跳过局部最小，也可以相对平稳
  2. 一些加速算法只能用在Batch模式下(如:conjugate gradient，hessian-based)
     可以现基于训练集学习得到一些加速算法需要的参数，再应用到Stochastic方法中，但是在Online就不行了(因为没有提前准备好的数据集)。
     
     

Momentum

• CM(Classical Momentum)
  $\hspace{8mm}v_{t+1} = \mu v_t - \epsilon f^{'}(\theta _t) \\ \hspace{8mm}\theta_{t+1} = \theta_t + v_{t+1}$

• NAG(Nesterov Accelerated Gradient)
  $\hspace{8mm}v_{t+1} = \mu v_t - \epsilon f^{'}(\theta _t + \mu v_t) \\ \hspace{8mm}\theta_{t+1} = \theta_t + v_{t+1}$
  其两者的图形比较如下:
  
  
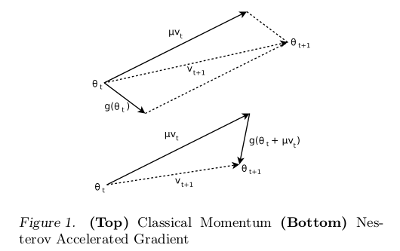
  1. 文章[2]中Ilya Stutskever使用文章[4]中Sparse Inilitialization，加上NAG达到了文章[4]中的HF的优化效果。
  2. 文章[2]中还指出尤其在$\mu$比较大时，NAG的效果更好
  3. bingo在文章[3]中又对NAG进行了进一步的解释(TODO::看一下)
• Simplified NAG(Nesterov Accelerated Gradient)
  原文见here。即在一个偏移的$\theta$上进行更新，详细的变动如下:
  $Set: \\ \hspace{8mm}\theta^{'}_{t} = \theta_t + \mu v_t \\ Then: \\ \hspace{8mm}v_{t+1} = \mu v_t - \epsilon f^{'}(\theta^{'}_t) \\ \hspace{8mm}\theta^{'}_{t+1} = \theta^{'}_t - \mu v_t + v_{t+1} + \mu v_{t+1}\\ \hspace{17mm}= \theta_t + v_{t+1} + \mu v_{t+1}\\ \hspace{17mm}= \theta^{'}_t - v_{t+1} - \epsilon f^{'}(\theta^{'}_t) + v_{t+1} + \mu v_{t+1}\\ \hspace{17mm}= \theta^{'}_{t} - \epsilon f^{'}(\theta^{'}_t) + \mu v_{t+1}$
  
  

Weights Initialization

• Lecun’s Advice
  $\hspace{8mm}stdv = 1/math.sqrt(L_{total_input_num}) \\ \hspace{8mm}w = torch.uniform(-stdv, stdv)$

• Andrew’s Advice
  $\hspace{8mm}epsilon = \sqrt{6}/\sqrt{L_{out}+L_{in}} \\ \hspace{8mm}w = torch.uniform(-epsilon, epsilon)$
  这里以输入层与一个隐层为例，$L_{in}$与$L_{out}$,是指神经网路的整个输入节点数，与与之相连的整个隐层的节点数。这里只适合全链接，不过还是上面的方法通用一点

• Sparse Initialization
  详细见文章[2]与[4]。其方法是随机的挑选一些链接，这些链接的参数采样之unit-gaussian(再加上一个缩放因子)。一般偏移取0，tanh激活函数的偏移取0.5。

idx = ceil(rand(1,numconn)*input_num);    
W{i}(j,idx) = randn(numconn,1)*initcoeff;    
此计算的是第i层的第j的节点的参数。numconn为链接的参数不为0的个数    <br />

Input Processing

详细分析见文章[1]

• 每次epoch都shuffle一下训练集
  神经网路只有在没遇到的训练样本下，学习才会很快， 因此当很多类似的样本在一起时，会降低网路的学习速度

• remove DC
  注意[mean normalize]也有remove DC的作用。举个极端的例子，当一个输入样本的所有值都为正时，这是与输入相连的一个节点的所有权重的更新为$\delta \vec x$(Delta rule),$\vec x$为输入变量。我们发现所有的权重的更新值的符号都是相同。也就是说权重只能通过zigzagging来改变方向。导致学习没有效率

• std normalize
  每一维的特征均值的方差为都拥有相同的方差。这样就把所有的特征的信息scale到同一个尺度上面了(不会有哪个特征重要，哪个特征不重要的情况发生)。当然这样做也有不好的地方，就是当知道哪些特征不重要时(其方差就应该比其他特征低一些)

• whiten
  每一维的特征之间不相关。（TODO:: 具体分析没看明白？）
  
  

Active Function

如下图:

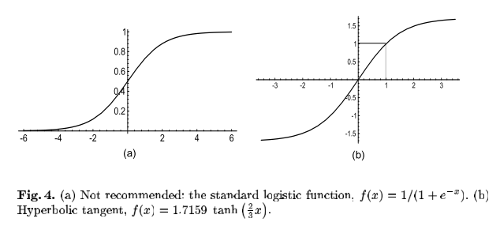
1. 一般建议使用左图的hyperbolic tangent函数，其输出关于原点对称。且其有效增益(即输出与输入的比为增益)为1，因此其输出值的方差接近1。符合样本处理中输入均值为0，且拥有相同方差的需求的分析
2. hyperbolic tangent函数的缺点是，其error surface在0点(0点初值为0，其变动比较小)与两个极端点初比较平坦， 即其有3个饱和的区域(左图只有在两端饱和)。 因此在参数初始化时，应避免参数的值比较小，落入到hyperbolic tangent的0点附近的饱和区
   
   

Learning Rate

• 每个权重都应有自己各自的学习率(所有2介导数的方法的目标)
• 神经网路的越是前几层的，其参数的学习率越要大
• 权重的学习率应该和节点的输入单元的个数的平方差成正比

References

1. Efficient BackProp
2. On the importance of initialization and momentum in deep learning
3. Advances in Optimizing Recurrent Networks
4. Deep learning via Hessian-free optimization