PCA(Principal Component Analysis)

PCA在图像与信号处理中应用非常广泛。主要用来进行降维与一些预处理。PCA处理后新的特征之间的将不相关性，即新的数据的协方差矩阵为对角阵。PCA可以理解为寻找一些表达了数据最大方差的线性特征, 其假设数据是符合Gaussian分布的(与ICA(./ica.html)正好相反)。 目标函数如下：
$\hspace{8mm}{Max}_W \hspace{6mm} var[\sum_{x,y}W(x,y)I(x,y)] \hspace{6mm} (1)\\ \hspace{16mm} 其中: \\ \hspace{20mm} W(x,y)所要求的一个主要成分，且||W(x,y)||_2 = 1 \\ \hspace{20mm} I(x,y)表示的是原数据 \\ \hspace{20mm} \sum_{x,y}W(x,y)W_j(x,y) = 0 \hspace{4mm}(W_j(x,y)为前面通过式(1)求得的主要成分)$

Solve

上面的优化问题可以通过数据的协方差矩阵的特征值分解来计算。步骤如下:

1. 计算数据的协方差矩阵M(如果各维度特征的量纲不在一个级别，可以除以标准差进行归一化,不会改变特征值，一般图像处理中不进行归一化)，并计算协方差矩阵的特征向量矩阵U和特征值$\lambda$(特征值的对角矩阵也是PCA旋转后协方差矩阵)
2. 将数据进行PCA投影，即$X_{pca}=U^TX_{ori}$

注意:

1. 特征向量的个数最多为MIN（n-1, p），其中n是样本的个数，p是特征的维数
   
   

Dimension Reduction

• 降维度操作
  即去除一些特征值比较小的特征向量进行PCA转换。 如下:
  $\hspace{8mm}X_{pca}=U_{part}^TX_{ori} \\ \hspace{16mm}其中: \\ \hspace{20mm}U_{part} \in R^{n*k} \\ \hspace{20mm}X_{roi} \in R^{n*1} \\ \hspace{20mm}X_{pca} \in R^{k*1} \\ $

• 维度的选取
  假如需要降维后的数据保留原数据99%的方差,即
  $\hspace{8mm}\frac{\frac{1}{m}\sum_{i=1}^{m}||x^{(i)}-x^{(i)}_{approx}||^2}{\frac{1}{m}\sum_{i=1}^m||x^{(i)}||^2} \le 0.01 \\ \hspace{16mm}其中: \\ \hspace{20mm}x_{approx}为重建后的特征$
  通过协方差矩阵的特征值来计算,即
  $\hspace{8mm}\frac{\sum_{i=1}^K\lambda_i}{\sum_{i=1}^m\lambda_i} \geq 0.99(假设\lambda按降序排列)$

• 降维后重建
  $\hspace{8mm}X_{approx} = U_{part}∗(U_{part}^T∗X)$
  因为是协方差矩阵是对角矩阵，所以U是正交矩阵。即$U^TU=I$。因此当没有进行降维时，数据是可以完全恢复的。

• 从统计的角度看降维
  
  1. 目标函数
     以2D->1D为例，寻找一个方向向量$\vec u$,使得数据投影到方向向量上的距离和最短。如果是3D->2D,则是寻找2个方向向量$\vec u_1, \vec u_2$, 因为两个向量可以组成一个平面, 如下图:
     
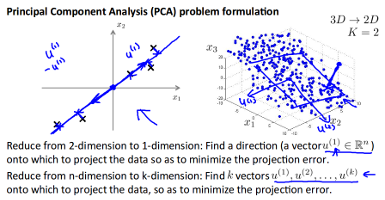
  2. 其和线性回归的区别
     线性回归是寻找其垂直方向上的距离和最短，而PCA是寻找其垂直投影到向量上的距离最短。如下图:
     
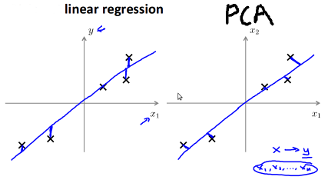
• 应用场景
  
  1. 降维来减少内存的消耗，以及提高性能
  2. 不能使用PCA降维来防止数据过拟合(Andrew NG的在机器学习公开课里有提到，但没说具体原因)。但其其实也可以作为一种regularization(见[3]p230，像L1、L2一样，表面上看其是降低了特征的维数，但其实其限制是通过一些线性组合来约束原特征空间的参数）
     
     

Whiten

详细见here

Reference

1. Natural Image Statistics(Chapter 5)
2. Machine Learning open course
3. An Introduction to Statistical Learning